Què és la beta (β) en els BJT

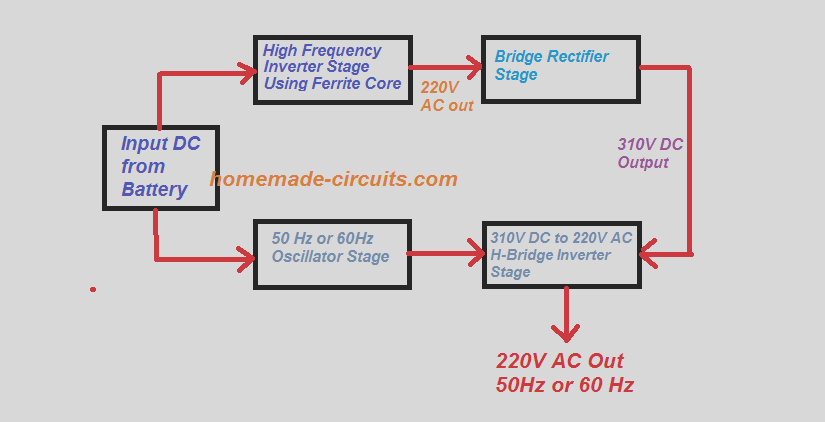
En els transistors de juntes bipolars, el factor que determina el nivell de sensibilitat del dispositiu a la base del corrent i el nivell d'amplificació del seu col·lector s'anomena beta o hFE. Això també determina el guany del dispositiu.

Dit d’una altra manera, si el BJT utilitza corrent relativament més alt per canviar òptimament la seva càrrega de col·lector, té una intensitat baixa b (beta), al contrari, si és capaç de canviar el corrent nominal del col·lector de forma òptima mitjançant un corrent base inferior, es considera que la seva beta és alta.

En aquest article parlarem sobre la versió beta ( b ) i què és hFE en configuracions de BJT. Trobarem la semblança entre les beta d’ac i de cc, i també demostrarem mitjançant fórmules per què el factor beta és tan important en els circuits BJT.

Un circuit BJT al dc bias mode forma una relació entre el seu col·lector i els corrents de base I C i jo B mitjançant una quantitat anomenada beta , i s’identifica amb la següent expressió:

b dc = Jo C / Jo B ------ (3.10)

on les quantitats s’estableixen en un punt de funcionament específic del gràfic característic.

En circuits de transistors reals, el valor de beta per a un determinat BJT normalment pot variar dins d’un rang de 50 a 400, on el rang mitjà aproximat és el valor més comú.

Aquests valors ens proporcionen una idea sobre la magnitud dels corrents entre el col·lector i la base del BJT.

Per ser més precisos, si s’especifica un BJT amb un valor beta de 200, significa que la capacitat del corrent de col·lector I C és 200 vegades més del corrent base I B.

Quan consulteu els fulls de dades, veureu que el fitxer b dc d'un transistor que es representa com a hFE.

En aquest terme la carta h està inspirat en la paraula híbrida com en transistor h circuit híbrid equivalent, en parlarem més sobre els nostres propers articles. Els subíndexs F a ( hFE ) s’extreu de la frase f amplificació de corrent cap endavant i el terme ÉS es pren de la frase common- és mitter en una configuració d’emissor comú BJT, respectivament.

Quan es tracta de corrent altern o corrent altern, la magnitud beta s’expressa com es mostra a continuació:

Formalment, el terme b a c es coneix com a factor d’amplificació de corrent directe d’emissor comú.

Com que en els circuits d’emissors comuns, el corrent del col·lector normalment es converteix en la sortida del circuit BJT i ​​el corrent base actua com l’entrada, el amplificació factor s’expressa tal com es mostra a la nomenclatura anterior.

El format de l’equació 3.11 s’assembla força al format de a i com es va comentar a la nostra anterior apartat 3.4 . En aquesta secció hem evitat el procediment per determinar el valor de a i a partir de les corbes de característiques a causa de la complexitat implicada de mesurar els canvis genuïns entre l’I C i jo ÉS sobre la corba.

No obstant això, per a l’equació 3.11 trobem que és possible explicar-ho amb certa claredat i, a més, també ens permet trobar el valor de a i a partir d’una derivació.

Als fulls de dades de BJT, b i normalment es mostra com hfe . Aquí podem veure que la diferència només es troba en la lletra del fe , que apareixen en minúscules en comparació amb les majúscules per a les quals s'utilitzava b dc. També aquí s'utilitza la lletra h per identificar el h com a la frase h circuit equivalent híbrid i fe es deriva de les frases f guany corrent cap endavant i és configuració mitter.

La Fig 3.14a mostra el millor mètode per implementar l'Eq.3.11 mitjançant un exemple numèric, amb un conjunt de característiques, i es torna a produir a la Fig. 3.17.

Ara anem a veure com podem determinar-ho b i per a una regió de les característiques identificades per un punt operatiu que té valors I B = 25 μa i V AIXIS = 7,5 V tal com es mostra a la figura 3.17.

La regla que restringeix V AIXIS = constant exigeix ​​que la línia vertical es dibuixi de manera que talli el punt de funcionament a V AIXIS = 7,5 V. Això fa que el valor V AIXIS = 7,5 V per romandre com a constant en tota aquesta línia vertical.

La variació en I B (ΔI B ) com es veu a l’equació. En conseqüència, es descriu 3.11 seleccionant un parell de punts als dos costats del punt Q (punt de funcionament) al llarg de l'eix vertical amb distàncies aproximadament uniformes a banda i banda del punt Q.

Per a la situació indicada, les corbes que impliquen les magnituds I B = 20 μA i 30 μA compleixen els requisits mantenint-se a prop del punt Q. A més, estableixen els nivells d’I B que es defineixen sense dificultat en lloc de requerir la necessitat d’interpolar l’I B nivell entre les corbes.

Pot ser important tenir en compte que els millors resultats es determinen normalment seleccionant ΔI B el més petit possible.

Podem esbrinar les dues magnituds de IC al lloc on es troben les dues interseccions de I B i l'eix vertical es creuen traçant una línia horitzontal a través de l'eix vertical i avaluant els valors resultants d'I C.

El b i establert per a la regió específica es podria identificar resolent la fórmula:

Els valors de b i i b DC es pot trobar raonablement a prop l’un de l’altre i, per tant, sovint es poden intercanviar. Significat si el valor de b i s’identifica, és possible que puguem utilitzar el mateix valor per avaluar b dc també.

Tot i així, recordeu que aquests valors poden variar segons els BJT, fins i tot si provenen del mateix lot o lot.

Normalment, la similitud en els valors de les dues beta depèn de la petita especificació de I Conseller delegat és per al transistor en particular. Més petit jo Conseller delegat presentarà una major similitud i viceversa.

Ja que la preferència és tenir menys jo Conseller delegat valor per a un BJT, la similitud de la dependència de les dues beta esdevé una ocurrència genuïna i acceptable.

Si tinguéssim la característica que apareix tal com es mostra a la figura 3.18, tindríem la b i similar a totes les regions de les característiques,

Es pot veure que el pas d’I B s'estableix a 10µA i les corbes tenen espais verticals idèntics en tots els punts de característiques, que és de 2 mA.

Si avaluem el valor de b i en el punt Q indicat, produiria el resultat com es mostra a continuació:

Això demostra que els valors de les beta ac i dc seran idèntics si la característica del BJT apareix com a la figura 3.1. Concretament, podem observar aquí que l’I Conseller delegat = 0µA

En la següent anàlisi, ignorarem els subíndexs AC o DC per a les beta només per mantenir els símbols simples i nets. Per tant, per a qualsevol configuració de BJT, el símbol β es considerarà beta com a càlcul tant de ca com de corrent continu.

Ja hem parlat sobre alfa en una de les nostres publicacions anteriors . Vegem ara com podem crear una relació entre l'alfa i la beta aplicant els principis fonamentals apresos fins ara.

Utilitzant β = I C / Jo B

aconseguim jo B = Jo C / β,

De manera similar, també per al terme alfa, podem deduir el valor següent:

α = jo C / Jo ÉS , i jo ÉS = Jo C / α

Per tant, substituint i reordenant els termes trobem la relació següent:

Els resultats anteriors són els indicats a Fig. 3.14a . La beta es converteix en un paràmetre crucial ja que ens permet identificar una relació directa entre les magnituds dels corrents a través de les etapes d’entrada i sortida per a una configuració d’emissor comú. Això es pot reconèixer a partir de les següents avaluacions:

D’aquesta manera es conclou la nostra anàlisi sobre què és beta a les configuracions de BJT. Si teniu algun suggeriment o informació addicional, compartiu-lo a la secció de comentaris.